Kenapa Penggunaan Float Bisa Berbahaya? Perbedaan Integer dan Float.

Tahukah kamu kalau float itu sangat berbahaya jika kamu tidak tahu cara menggunakannya? Kamu bisa jadi kehilangan uang bahkan menghilangkan nyawa orang. Cerita ini bukan karangan semata, kesalahan penggunaan float dapat berakibat fatal.

Perbedaan antara integer dan float bukan sekadar bilangan bulat dan bilangan pecahan!

Kenapa menggunakan float tanpa tahu seluk beluknya bisa berbahaya?

Sekilas Cara Komputer Bekerja

Komputer bekerja menggunakan listrik. Listrik yang diterima akan diubah oleh komputer menjadi sinyal. Sinyal tersebut akan diubah menjadi dua angka yakni 0 dan 1. Angka 0 terjadi ketika voltase listrik berada di bawah suatu batas mendekati 0. Angka 1 terjadi ketika voltase listrik berada di atas batas.

Dari sini, kita bisa melihat bahwa komputer hanya mengetahui dua angka yakni 0 dan 1 yang disebut angka biner.

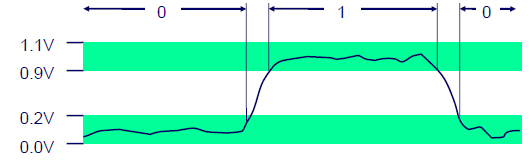
Untuk dapat menghasilkan data lain selain angka 0 dan 1, komputer melakukan yang namanya representasi. Beberapa contoh representasi biner yang terjadi di komputer:

1. Representasi bilangan bulat desimal. Dimana deretan angka biner diubah ke bentuk bulat. Contoh angka biner 1101 direpresentasikan sebagai 13 dalam bilangan bulat.

2. Representasi huruf. Dimana deretan angka biner diubah ke huruf alfabet. Contoh angka biner 1000001 direpresentasikan sebagai huruf ‘A’ dalam standar ASCII.

Poin pentingnya adalah komputer hanya mengerti angka biner: 0 dan 1. Seluruh data dalam bentuk lain hanya merupakan representasi yang dibuat oleh manusia.

Representasi Integer vs Float dalam Bit

Karena komputer hanya mengerti angka biner (0 dan 1), manusia membuat kesepakatan dalam membaca (merepresentasikan) angka-angka biner tersebut. Dibagian ini hanya akan dibahas sekilas representasi integer dan float. Namun, masih banyak jenis data lain yang memiliki aturan representasinya sendiri-sendiri (contoh: standar ASCII).

Representasi Integer

Untuk mengubah angka biner (0 dan 1) menjadi bilangan bulat (integer), telah disepakati digunakan base-2 numbering system.

Pertama kita lihat angka yang kita gunakan sehari-hari. Angka yang kita gunakan sehari-hari disebut sebagai base-10 numbering system. Angka ini terdiri dari 10 jenis angka (dari 0 sampai 9). Kita bisa menuliskan angka tersebut menjadi persamaan berikut ini,

Pada base-10 numbering system, pengali akan naik 10 kali setiap bergeser satu angka ke kiri. Kita dapat juga melakukan hal yang sama pada base-2 numbering system.

Untuk mengubah angka biner 1101 ke angka bulat desimal, kita dapat menggunakan cara diatas,

Representasi integer dalam komputer disepakati menggunakan base-2 numbering system. Tidak ada yang aneh disini.

Representasi Float dan Double

Masalah muncul ketika kita ingin merepresentasikan bilangan pecahan ke dalam bentuk biner.

Beruntungnya, organisasi IEEE membuat standar yang dapat menyelesaikan masalah ini. Standar tersebut bernama IEEE 754 Standard for Floating-Point Arithmetic.

Bagaimana bentuk biner dari sebuah pecahan menurut standar tersebut?

Gambar diatas merupakan representasi pecahan dalam bentuk biner untuk tipe float (32-bit). Biner dipecah menjadi 3 bagian yakni:

• Sign. Menentukan apakah angka tersebut negatif (jika 1) atau positif (jika 0).
• Exponent. Menentukan pengali dalam bentuk dua pangkat sekian.
• Fraction. Menentukan angka yang dikalikan.

Representasi bit tersebut akan dibaca dalam bentuk bilangan dalam notasi ilmiah:

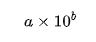
Pada tipe double (64-bit), kurang lebih representasinya mirip hanya berbeda pada jumlah exponent dan fraction.

Artikel ini tidak akan membahas detil mengenai perhitungan floating-point ini. Jika kamu ingin mempelajarinya bisa membuka halaman wikipedia untuk IEEE 754.

Masalah Pada Representasi Float dan Double

Bilangan pecahan memiliki jumlah yang terhingga. Contohnya di antara 0,1 dan 0,2 terdapat tak terhingga bilangan pecahan yang ada seperti 0.15, 0.1222, dst. Sehingga, representasi IEEE 754 di atas tidak mungkin mencakup seluruh bilangan pecahan yang ada.

Masalah tersebut membuat terjadinya pembulatan pada angka-angka yang tidak dapat direpresentasikan dalam bentuk biner. Mari kita lihat contoh berikut.

Dalam bentuk float (32-bit),

Angka pecahan 0.10000000149 direpresentasikan sebagai 00111101110011001100110011001101

Jika kita mengurangi 1 bit di bagian akhir, maka binernya akan menjadi 00111101110011001100110011001100

Jika biner tersebut diubah ke angka pecahan akan menjadi 0.0999999940395.

Dari sini, kita bisa melihat bahwa tidak ada representasi yang benar-benar tepat untuk angka 0.100000000000.

Menyebabkan komputer harus menggunakan representasi biner untuk angka 0.10000000149 sebagai gantinya. Disini, secara tidak langsung terjadilah pembulatan.

Singkatnya, karena adanya pergeseran atau pembulatan tersebut, nilai yang dihasilkan juga ikut bergeser. Semakin banyak operasi floating-point yang kamu lakukan, kesalahannya akan semakin besar.

Catatan: Penjelasan ini dibuat sesederhana mungkin tanpa menggunakan perhitungan kompleks. Kamu bisa membuktikannya sendiri dengan menghitung bit addition dari kedua nilai float.

Contoh Pada Berbagai Bahasa Pemrograman

Contoh diambil dari situs 0.30000000000000004.com.

Pada contoh di bawah ini, seluruh angka pecahan menggunakan tipe double (64-bit), bukan float. Namun, pada dasarnya keduannya sama hanya berbeda tingkat presisi.  

C

#include <stdio.h>

int main(int argc, char** argv) {
  printf("%.17f\n", .1 + .2);
  return 0;
}

0.30000000000000004

Python 3

print(.1 + .2)

0.30000000000000004

PHP

var_dump(.1 + .2);

float(0.30000000000000004441)

Javascript

console.log(.1 + .2);

0.30000000000000004

Penggunaan Float yang Harus Dihindari

Jika perhitungan yang kamu lakukan membutuhkan akurasi tinggi, jangan pernah menggunakan float atau double. Contoh perhitungan yang membutuhkan akurasi tinggi adalah keuangan. Misalkan kamu memiliki website jual-beli online, jangan menggunakan float untuk perhitungan uang. Perhitunganmu lama kelamaan bisa meleset jauh dari yang seharusnya.

Jika kamu ragu, jangan pernah gunakan float.

Kasus-Kasus yang Terjadi Akibat Kesalahan Penggunaan Float

Ledakan Ariane 5 Test Flight (1996)

Ariane 5 adalah roket yang dibuat oleh European Space Agency (ESA) yang bertugas untuk mengirimkan muatan ke orbit. Pada saat uji penerbangan pertama, roket ini meledak dan mengakibatkan kerugian mencapai 500 juta US Dollar. Penyebab ledakan ini adalah karena adanya konversi data dari tipe float 64-bit ke tipe integer 16-bit. Kedua tipe ini sangat berbeda dan menyebabkan error pada operasi di prosesor roket.

Ketidak-akuratan MIM-104 Patriot Missile (1991)

Peluru ini menggunakan float pada sistemnya untuk sistem radar dan targetnya. Karena adanya akumulasi error yang disebabkan oleh pembulatan / pergeseran nilai float yang tidak diperbaiki, terjadi kesalahan perhitungan target. Menyebabkan 28 orang meninggal karena peluru ditembakkan ke koordinat yang salah.

Bahan Bacaan Lanjutan

[1] Carnegie Mellon University, 18-213 Introduction to Computer Systems: Floating Point

[2] Rob Kennedy. What is the exact value of a floating-point variable?